The Giant Cultural Parasite, Part 4
The big picture (Part 1):
The systems that drive our culture and determine our lives are out of control and seem to have their own agendas.
Where we’re at:
In Part 2, we considered how natural laws create patterns, like how water moves under pressure from a stone, and we saw how forces like gravity and momentum create repeating cycles of movement—oscillations—that create patterns like waves.
In part 3, we explored how self-replicating structures like canyons and salts emerge out of a tendency for different objects to fit themselves to one another and to shape each other to fit even better.
In this part (4), we’ll take a look at how and why self-replicating structures dominate the world, which will answer the question “why is there order instead of chaos?” We’ll explore Richard Dawkins’ laws of replication and explain why they work the way they do. Keep your eyes open for a law that seems to be missing, which I believe has big implications for better explaining the world we live in today.
In part 5 and onwards, we’ll talk about how competition for resources led to greater complexity and “goals”, and how the world of ideas, consciousness, and systems emerged. Then we’ll talk about why systems have their own goals, based in the same competition for resources that engages individuals and species, and how we might be able to use this understanding—in a fancy bit of inverted logic—in order to shape the systems to our own ends.
Here we go.

So why do replicators dominate?
Although we’ve seen—using salt crystals and the oscillation of waves—that replication doesn’t require any great complexity, it’s clear that life in the world as we know it is complex. So how did we get here?
Rather than start at the beginning and try to come up with laws that would create today’s world, it might be easier to start with today and work our way backwards. This is a thinking tool called reversal or inversion, and it’s how many of our most important theories were derived.
In order for something to exist today, there are only two possible routes it could follow. Either it was here before, or it wasn’t. If it was here before, then it lasted. If it wasn’t here before, it must have been created (I’m using this term in a very loose sense that simply means it didn’t exist before. This argument doesn’t require a divine creator, nor does it disprove one.)
So we start with two options:
- 1-Lasted
- 2-Created
If it lasted, it’s the same. But created objects can either be something brand new, or derived from something that came before. We can split created objects into two new categories, like so:
- 1-Lasted
- 2a-Created (new)
- 2b-Created (from something that came before: “old”)
We’ve already seen how some phenomena come from what came before; these are our replicators (2b). They can be further divided into: (2b1) an exact copy of something that came before; (2b2) a variation on something that came before; or (2b3) a melding of two or more things that came before. So now we have 5 categories of phenomena:
- 1-Lasted
- 2a-Created (new)
- 2b1-Created (old)—exact copy
- 2b2-Created (old)—variation on something old
- 2b3—Created (old)—melding of 2 or more old things
I want to tease ahead a little bit and point out that this is true not only of physical phenomena, like rocks and planetary orbits and bacteria and elephants and your great-uncle Albert, but also of mental phenomena like alphabets and laws and economic systems and utterly obnoxious sayings like “it is what it is”.
So we can see that every existing phenomena must have come to be in the present moment by one of these five principles. Let’s renumber and simplify:
- A-Lasted
- B-New Creation
- C-Exact Copy
- D-Variation
- E-Melding
To reiterate, strategies C, D, and E are our replicators.
If we begin with a random number of each type of phenomena, how would they fare? Let’s say we start with one of each and go through 5 generations. How many of each would we have?
A-Lasted: Things that last, continue to last. Since there are no copies made, you continue to have 1 instance of A after 5 generations.
B-New Creation: Since each generation brings a brand new creation with no relation to the old creation, B disappears and something new takes its place. Generation 2 is R, 3 is W, 4 is H, 5 is N (I chose letters at random). You have one instance of N and no instances of B (or R, W, or H). Complete randomness and chaos.
C-Exact Copy: Each generation, the original C is replaced by a new copy of C. Generation 2 is C, 3 is C, 4 is C, 5 is C. We still have one C.
D-Variation: D is replaced by a different version of D, which we’ll call D-prime (D’). Generation 2 is D’, 3 is D’’, 4 is D’’’, 5 is D’’’’. We have something similar to D that is mostly, but not quite the same. Let’s say that each generation is 80% of the generation before it. We end up with only 41% of D left after 5 generations.
E-Melding: E combines with something else. Generation 2 is [EF], 3 is [EFGH], 4 is [EFGHIJKL], 5 is [EFGHIJKLMNOPQRST]. We still have part of E, but by generation 5 it’s only a small part of the original phenomena. In the abiotic world, we often see this in rocks, which are melded by heat and pressure. Let’s say that we have 5% of E.
Here’s what we have so far:
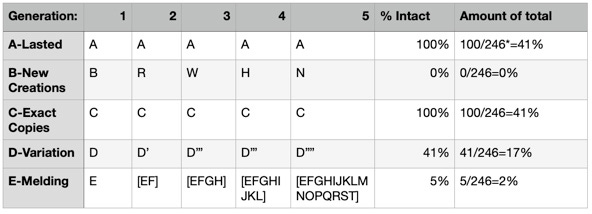
Even though the 80% and 5% numbers are estimates, you can see how some “strategies” (D and E) water themselves down, some immediately result in extinction (B), and how other strategies carry themselves through the generations more effectively. Longevity (strategy A) and Fidelity (strategy C) are the strongest strategies, and we should have lots of phenomena that last, and lots that are exact copies of themselves, assuming that those strategies can be deployed with absolute perfection. But even if we can agree that perfect longevity and perfect fidelity seem to be impossible in the universe we live in, we can still see that they are clearly good strategies.

But wait a second. What if we assume that the our replicators (C, D, and E) can proliferate more than one at a time? Let’s assume they can have 2 “babies” each generation. Let’s see what happens.
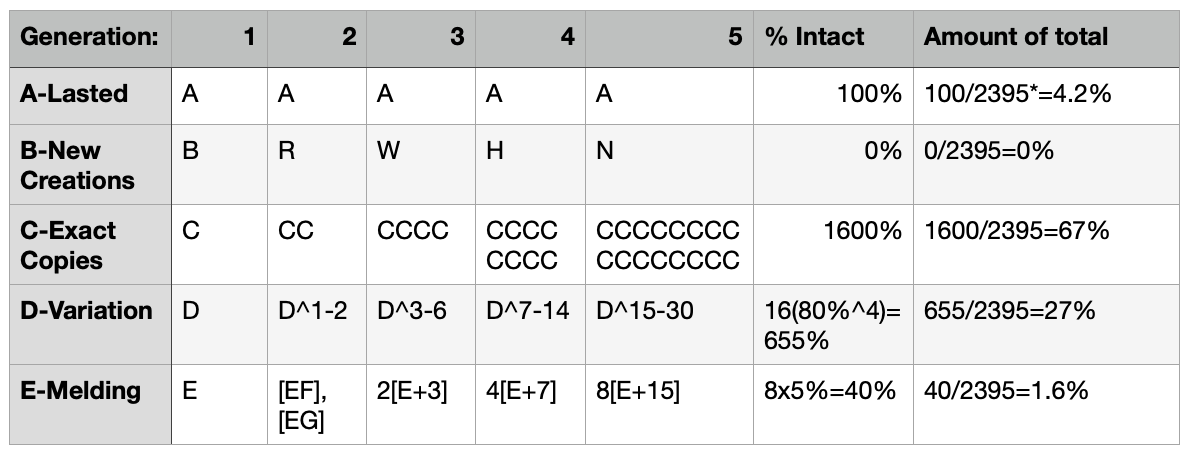
I know this looks complicated, but the main idea is actually pretty straightforward: For C, more copies equals more of the phenomena (16 exact copies of C). For D, more copies of a slightly diluted phenomena (80% of D to get D’ and D’’, then 80% of each of those to get the next generation, and so forth) gives us more in total of the phenomena. For E, more copies of a heavily diluted phenomena still gives us less, but more than it would have otherwise. The most important takeaway here is how the final percentages of this model compares to the previous model.
What really pops here is how poorly longevity (Strategy A) does in this situation. With this one simple tweak (doubling replication), our replicators (C,D, and E) have shoved Strategy A onto the sideline after only 5 generations. After a hundred generations, the A’s would be virtually a rounding error away from zero.
What we’re seeing here is the difference between linear growth (the first model) and exponential growth (the second model). In a universe where some things replicate, they will quickly outnumber the things that don’t. Things that are fecund (make more copies of themselves) will outnumber things that are not (make fewer copies of themselves). And, all else being equal, things that have high fidelity (make more exact copies of themselves) will outnumber the ones that have low fidelity (copy themselves with lots of variations). Of course, all else isn’t equal, but we’ll get to that.

So now we know why replicators dominate our world. Even if we were to change the initial number of each so that new creations (B) and long-lasting phenomena (A) outnumbered the replicators a hundred to one, or even a billion to one, exponential growth would eventually overtake linear growth, and we’d return to a universe overrun by replicators.
We’ve also discovered two of the laws that determine a replicator’s success: Fecundity and Fidelity.
Now let’s talk about Strategy A (longevity) for a moment. While it’s true that it doesn’t do so hot against things that replicate, we need to remember that all of these “strategies” are just different ways that phenomena arrive in the present. Everything in the perceivable universe has some amount of longevity, or else we wouldn’t be able to register it. And so far as we know, nothing observable has perfect longevity (and if it did, how would we observe its eternity?). So really, what we’re dealing with here is a continuum of relative longevity, where some things last longer than others.
That’s true of any of the other phenomena, whether they are new creations (B) or the replicators (C,D, and E). When we combine longevity with replication, we give the replicators more time to reproduce. So Longevity is another successful strategy for proliferation, but only when it’s combined with a replicator strategy.
As far as new creations (B) go, I don’t think anyone can say with any confidence whether entirely new creations have popped into existence from time to time. The Big Bang does seem to be one example. But even if they did show up occasionally, or even often, they would be quickly shouldered aside by the growth of the replicators, even if they had massive longevity.
So this week we’ve taken care of the central question of how and why replicators dominate the universe. We’ve also derived Richard Dawkins’ three laws of replicator competition: Fidelity (how exact are the copies?), Fecundity (how quickly does it make copies of itself”?), and Longevity (for how long can the replicator make more copies of itself?). Those laws are the basis for the next part of this series, where we’ll talk about how replicators compete for resources (Natural Selection), and how that leads to complexity that is beyond imagination.
Since the end goal of this series is to talk about how ideas and systems replicate and create their own goals (often unrelated to human goals), I should point out that although this is the basis for Darwin’s Theory of Natural Selection and is most often used to describe life, these principles remain the same regardless of whether we’re talking about trees, mathematical patterns, planetary orbits, computer code, or knock-knock jokes.
Until next time.